2024. 1. 30. 17:47ㆍ학습/머신러닝

01 기초 강의 목차 > 이후 심화 강의로
- 선형회귀
- 회귀분석 평가 지표
- 선형회귀 적용
- 선형회귀 심화
- 로지스틱회귀 - 타이타닉 생존 분류 문제
- 로지스틱회귀 이론(1)
- 로지스틱회귀 실습
- 다중 로지스틱회귀
- 로지스틱회귀 마무리
02 선형회귀
1. 학습 목표
회귀분식의 개념과 평가척도가 무엇인지 알아보자.
2. 선형회귀의 사례
1차 방정식을 배운 고등학생을 기준으로 설명한다.
방법 1) 실제 데이터 값 - 직선의 예측 값(직선은 예측하는 값의 집합) = Error라고 정의한다.
방법 2) 양/음수 때문에 절대적으로 양수로 만들기 위해 (절댓값은 계산이 어렵대) 제곱한다.
방법 3) 데이터는 자꾸 추가될 거니까 전체 에러 합을 데이터 개수로 나눠준다.
3. 선형회귀 이론
배웠던 일차 방정식으로 데이터 사이언스적으로만 바꿔보도록 한다.
✏️공통
Y는 내가 알고 싶은 값, 종속 변수(X의 영향 받음), 결과 변수
X는 Y에 영향을 주는 특정값, 독립 변수, 원인 변수
머신러닝과 통계학에서는 같은 원리지만 다른 용어를 사용한다.
✏️1. 통계학에서의 선형회귀 식

1) 편향 : 치우쳐져 있다.
2) 회귀 계수
3) 오차(에러), 모델이 설명하지 못하는 Y의 변동성이란? 사진 참고

✏️2. 머신러닝/딥러닝에서는?

베타와 에러를 합쳐서 "편향"이라고 부른다.
가중치를 웨이트의 약자인 "w"를 쓴다.
사실상 대응되는 식이다.
이유 : 딥러닝 모델에서는 오차 항은 명시적으로 다루지 않기 때문
✏️결국 두 수식이 전달하는 의미는?
회귀 계수 혹은 가중치를 알면 "X"가 주어졌을 때 "Y"를 알 수 있다는 것이다💡
우리는 편의를 위해 X의 계수를 가중치라고 지칭한다.
= 추정치와 편향을 알고 있으면 몸무게(X)가 들어가면 키(Y)의 근삿값을 알 수 있다.
(스포) 키와 몸무게 데이터를 이용해서 선형회귀 식을 만들면
y = 0.86x + 109.37 이 나온다.
이론의 장점 : x값이 있으면 y값도 알 수 있고, 기울기 혹은 가중치 해석이 중요하다.
- 기울기 해석
- x가 1kg 증가할 때, y가 얼마나 증가하는지 알기 위해서는 식의 기울기를 보면 된다.
- 기울기는 x의 계수인 0.86이다.
- 따라서 1kg 증가할 때마다 키가 0.86cm 증가한다.는 것으로 해석할 수 있다.
💡우리가 만든 몸무게와 키에 대한 선형회귀식은 진실한 값이 아닐 수도 있다.
→ 일반적인 식을 만들면 이렇게 해석할 수 있고 이것이 선형회귀의 강력함이다.
+ 기울기 설명 추가
- 주어진 선형 방정식의 기울기는 x의 계수이며,
- 일반적으로 선형 방정식에서 x의 계수는 해당 변수의 변화에 따른 종속 변수의 변화량을 나타낸다.
- 여기에서 주어진 식인 y = 0.86x + 109.37에서 x의 계수는 0.86이다.
- 따라서 x가 1kg 증가할 때, y는 0.86만큼 증가한다.
질문 1. 베타제로는 1차 방정식의 y 절편에 해당하는 건 알겠다. 근데 에러(e)는 왜 따로 있나?
우리가 식을 만들었지만 해당 식이 모든 데이터를 설명할 수 없음.
우리가 그린 선 위에 모든 실제 데이터가 있다는 경우는 아예 없음.
실제 데이터랑 예측 데이터랑 같은 경우는 없기에 에러를 통해서 보완을 해준다.
모델의 오차는 늘 있을 수 있으니까.
질문 2. 머신/딥러닝에서 가중치를 알게 되면 (혹은 회귀식에서 베타를 알게 되면)
x값에 대해서 y값을 예측할 수 있다는 건 이해했다. 그럼 가중치(베타)는 어떻게 구하나요?
머신러닝을 관통하는 질문이다. 데이터가 충분하다면 가중치(추정치)를 "추정"할 수 있다.
추정한다는 건 예측, 구한다는 말과 상통한다. 이 내용은 심화 내용이다.
지금은 그냥 현재 그래프를 수없이 그려서 에러를 "최소화"하는 직선을 구한다고 생각하면 된다.
여기까지 선형회귀를 수립하는 방법에 대해 배웠다.
4. 회귀 분석의 평가지표
해당 모델이 좋은지 평가하는 방법도 알아본다.
✏️선형회귀란?
직선으로 표현하기 때문에 선형이란 말을 쓰고
회귀라는 것은 돌아가다라는 의미잖아.
분포된 점들(실제 데이터들)이 주변에 퍼져있어서
선으로 군집하려는, 돌아가려는 모양인 것처럼 보인다고 해서
회귀라는 단어를 쓴다고 한다.
직선이지만, 방정식이긴 하지만 모델이라고 부를 수 있다.
✏️모델을 평가하는 방법을 알아보도록 하자.
평가지표에는 MSE라는 게 있다.
일단 에러 정의 방법을 다시 보자면
1) 에러를 정의한다. 에러 = 실제데이터-예측데이터
문제 = 음수, 양수를 더하면 상쇄되는 문제가 있었다.
2) 양수를 만들기 위해 다 제곱하고 합쳤다.
문제 = 데이터가 많아질수록 에러가 자연스레 커지는 현상이 있었다.
3) 데이터 수만큼 나눠서 보정했다.
✏️수식화를 하면 아래처럼 된다.

✏️방법별 세부 설명 들어간다.
방법1
y(키) : 혼자 동떨어져 있으면 실제 값 (True값)
i가 붙은 이유 : 데이터가 여러개여서 그렇다.
^(hat) : 예측 혹은 추정한 값을 표기하는 방법. 진짜 값을 알 수 없지만 직선을 통해 추정한 값.
Q. y가 왜 들어가지 x아닌가? 몸무게가 들어가는거 아닌가 수직값인데?
A. 자문자답 근데 구하고 싶은게 키 값이지. 다시 앞부분을 복습하자.
(추가 설명하자면 y데이터는 값(실제값, True값)인데 우리 데이터에서 height일 뿐이다.)
상황 : 몸무게와 키의 데이터를 획득했고 일정하게 증가하는 패턴이 있다.
문제 정의 : 몸무게를 알면 "키"를 알 수 있을 것이다.
weights = [87, 81, 82, 92, 90, 61, 86, 66, 69, 69]
heights = [187, 174, 179, 192, 188, 160, 179, 168, 168, 174]
두 데이터를 가장 쉽게 보는 첫 번째 방법은 산점도를 그리는 것이었지.
1차 방정식 개념을 적용하려고 했지만 수많은 점들 중에 어떤 두 점을 이어 직선을 만들지 고민...
많은 점을 통과하는 여러 개의 직선을 그려보고자 했지.
눈 대중으로는 알겠는데 가장 적절한 그래프인지 알 수 없어서 data scientific한 발상을 떠올렸다.
💡직선과 점의 거리를 계산하는 것이었다. 이것을 Error라고 정의하고 최소의 에러인 직선을 그려보고자 했다.
방법 1) 실제 데이터 값 - 직선의 예측 값 = Error
- 1번 실제 데이터 187, 예측 데이터 187, Error 0
- 1번 실제 데이터 174, 예측 데이터 181, Error -7 (뭐에서 뭘 뺄지 순서 상관없지만 기준을 같이 해줌)
- 1번 실제 데이터 174, 예측 데이터 169, Error +5
모든 점에 대해서 Error를 다 계산할 수 있어졌다.
이 값을 제일 최소화하면 점들을 제일 잘 설명하는 직선이라고 할 수 있겠다.
방법2
i에 1부터 n까지 넣고 더함.
방법 1의 식에 제곱을 한 값을 모두 더하는 공식
방법3
데이터수=n으로 나눈다.
이거를 우리가 Mean Squared Error(MSE)라고 정의한다.
= 거꾸로 해석하면 "에러인데 제곱을 했고 평균"을 냈다.

💡앞으로 만날 숫자 예측 문제는 모델을 머신러닝이든 딥러닝이든 어떤 모델을 만들어도
항상 MSE 지표를 최소화하는 방향으로 진행하고 평하게 될 것이다!
왜? 어떤 특정 값이 있고 숫자를 맞추는 문제에서는
원래 실제 값이 있고 - 예측 값이 있잖아. 빼고 제곱해서 나누는 값을 정의할 것이다.
자세하게 배운 이유는
다른 어떤 숫자를 맞추는 회귀 모델에서는 다 위의 지표를 쓰기 때문이다.
✏️이거 말고 다른 지표가 있을 수 있다. (별 건 아님)
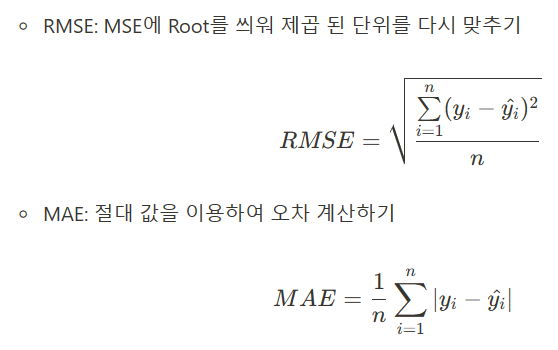
1) 루트를 씌우는 이유는 값이 제곱한 값에 루트를 씌우면 줄여버릴 수 있으니까
2) 절대 값을 이용하는 경우도 있다고 했는데 그 공식임.
뭘 사용해도 상관은 없는데 일반적으로 우리가 사용하게 될 라이브러리에서는 MSE
4. 선형회귀만 있는 지표 - R Square
다음 페이지로 (노트 필기)
'학습 > 머신러닝' 카테고리의 다른 글
| Machine Learning 6 : 로지스틱회귀 (0) | 2024.02.01 |
|---|---|
| Machine Learning 5 : 다중선형회귀, 실습 (0) | 2024.02.01 |
| Machine Learning 4 : R-Square (0) | 2024.02.01 |
| Machine Learning 2 : 주피터 노트북 (0) | 2024.01.30 |
| Machine Learning 1 : 머신러닝 (1) | 2024.01.30 |